Hướng dẫn làm Đáp án Ôn thi Cao học Học viện ngân hàng T4.2018
Lời nói đầu
Lịch thi cao học Học viện ngân hàng là vào trung tuần của tháng 4 này, Do đó, áp lực về việc ôn thi cao học đang ngày càng gia tăng. Những bạn kiến thức còn chưa chắc hoặc cần hệ thống thì CẦN THIẾT phải có những bài viết hướng dẫn chi tiết và cụ thể để giúp các bạn tổng ôn lại kiến thức. Trung tâm Ôn thi cao học Centre Train đã có rất nhiều bài viết chất lượng cho kỳ thi cao học Học viện Ngân hàng T4.2018. Tuy nhiên, Triết lý cốt lõi của trung tâm là ”Cầm tay chỉ việc” cho từng học viên và Ôn luyện thi bài bản từ A --> Z cho các môn thi. Mục tiêu của trung tâm là có 1 bài viết SIÊU CHẤT LƯỢNG phục vụ nhu cầu học tập của thí sinh đi thi năm nay.
Tham khảo: Kinh nghiệm Ôn thi cao học môn Xác suất thống kê
Bài viết sau đây về: Hướng dẫn làm Đáp án thi Cao học Học viện ngân hàng T4.2018 sẽ được Thầy Mạnh hướng dẫn một cách chuyên sâu.
1. Đáp án thi học phần Xác suất thống kê
Cấu tạo chung của đề thi môn toán Cao học Học viện ngân hàng là có 5 câu. Trong đó phần Quy hoạch tuyến tính là có 2 câu chiếm 4 điểm, phần xác suất thống kê chia làm 3 câu mỗi câu 2 điểm. Có thể thấy tỷ trọng đề thi thì môn Xác suất thống kê chiếm 60% trong tổng số điểm. Do đó, làm tốt phần này sẽ giúp thí sinh có điểm số khá cao.
Sau đây các bạn xem chi tiết từng câu:
CÂU 3 (2điểm): Đề thi ra xác suất cổ điểm (2 điểm) và nội dung thi phần xác suất cổ điểm có 3 dạng. Thường thì đề thi sẽ ra 2 trong 3 dạng hoặc cả 3 dạng:
- Dạng 1: Định lý cộng và nhân xác suất (4 Bước). Dấu hiệu nhận biết dạng 1 là đề bài cho 2 biến cố độc lập
- Dạng 2: Bài toán Bernoulli. Dấu hiệu nhận biết dạng 2 là bài toán cho n phép thử độc lập.
- Dạng 3: Công thức xác suất đầy đủ và Bayes. Dấu hiệu nhận biết dạng 3 là bài toán cho các biến cố có tổng xác suất các giả thuyết H1, H2, H3 là 100%. Và câu hỏi phụ có ghi giả sử Biến cố A xảy ra.
Xem hình:

Để làm tốt phần xác suất cổ điển các bạn tham khảo bài viết chi tiết:
Hướng dẫn ôn thi Cao học Đại học Quốc gia Hà nội T4.2018
Video: Bài giảng xác suất cổ điển (3 dạng thi):
- Các câu tiếp theo thì đề thi sẽ ra ở các khả năng sau (trung tâm sẽ khái quát toàn bộ đề thi năm nay dưới dạng các câu).
Câu 4 (2 điểm): Các dạng thi được liệt kê cụ thể như sau:
(sẽ giúp các bạn tổng ôn dễ dàng hơn):
Kịch bản 1: Đề cho 2 bảng phân phối xác suất của biến ngẫu nhiên rời rạc
Tìm Kỳ vọng toán
Tìm phương sai
Kịch bản 2: Đề cho hàm mật độ xác suất của biến ngẫu nhiên liên tục
Tìm tham số k
Tìm xác suất để Biến ngẫu nhiên X nhận giá trị trong khoảng (a, b)
Tìm Kỳ vọng toán và phương sai của hàm mật độ
Kịch bản 3: Cho biến ngẫu nhiên X phân phối chuẩn N(μ, σ2 )
Tìm P(a < X < b ) = ?
Tìm P (X > a) = ?
Kết hợp với Bernoulli
Xem hình:

Câu 5 (2 điểm): Suy diễn, ước lượng, kiểm định như sau:
2. Đáp án thi học phần Suy diễn
Phần Suy diễn của cao học học viện ngân hàng cũng nằm trong nội dung, hay thi nên chúng ta cũng nên học hết. Nếu đề có ra phần Suy diễn sẽ chiếm 1 điểm.
Nội dung thi về suy diễn:
- Trung bình mẫu X ngang
- Phương sai mẫu S2
- Tần suất mẫu f
Lưu ý: Đối với dạng bài toán suy diễn thì khi đọc bài các bạn phải hết sức chú ý là đề cho tham số mẫu hay tổng thể.
Ví dụ: Điều tra ngẫu nhiên thu nhập của 100 hộ gia đình ở khu dân cư A ta có số liệu sau. Thì đề bài đang cho các số liệu của tham số mẫu.
Trong hình là bài toán suy diễn:

3. Đáp án thi học phần Ước lượng
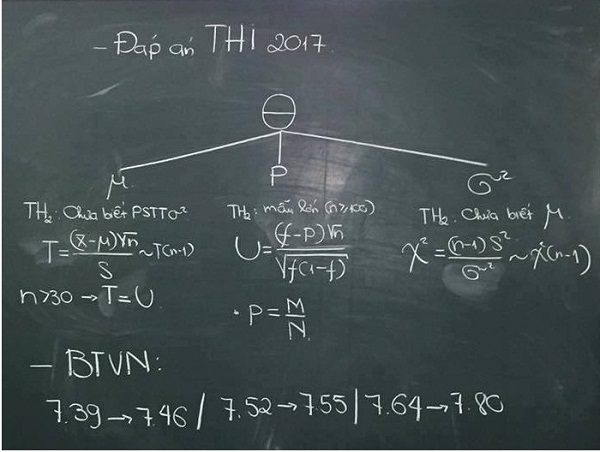
Đề thi chắc chắn có từ 2 đến 3 câu Ước lượng là được lấy trong một số các tham số: μ, P và σ2. Do giới hạn đề cương ra đã giảm rất nhiều kiến thức nên thực ra các bạn chỉ học có đúng 3 công thức sau:
Nội dung thi về ước lượng:
1. Trung bình tổng thể μ, 2. Cơ cấu của tổng thể P, 3. Phương sai tổng thể σ2.
- Dạng 1: Ước lượng trung bình tổng thể μ
- TH1: Khi đã biết Phương sai tổng thể σ2
- TH2: Khi chưa biết Phương sai tổng thể σ2
- Dạng 2: Ước lượng cơ cấu của tổng thể P (kích thước mẫu lớn, mẫu nhỏ) nhưng đề thi chỉ ra mẫu lớn n > = 100.
- Dạng 3: Ước lượng Phương sai tổng thể σ2
Xem hình:
Video: Bài giảng chuyên sâu học phần Ước lượng
Tham khảo các trình bày một bài thi đạt điểm max học phần Ước lượng ở đây:
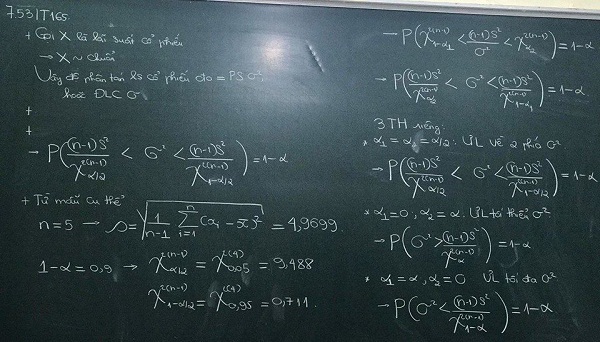
4. Đáp án thi học phần kiểm định
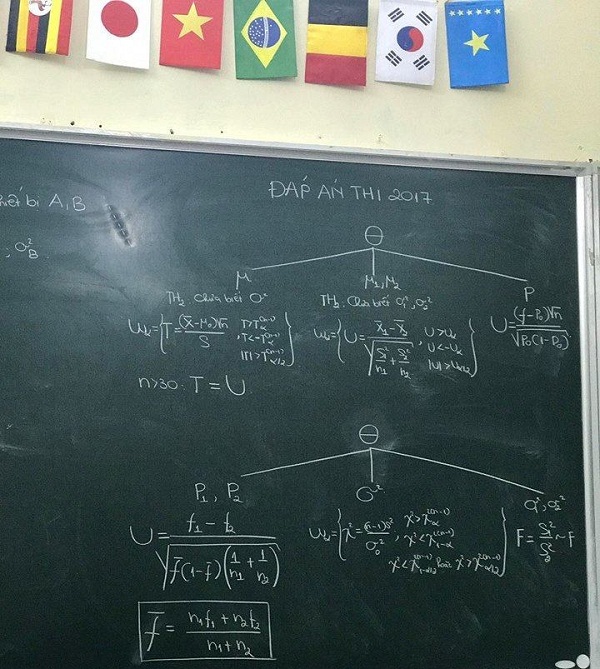
Học phần kiểm định có lẽ là nhiều công thức nhất phải học, các bạn sẽ phải học 6 công thức và chia làm 6 dạng Kiểm định giả thiết:
Nội dung thi:
- Dạng 1: Kiểm định 1 trung bình tổng thể μ
- TH1: Khi đã biết Phương sai tổng thể σ2
- TH2: Khi chưa biết Phương sai tổng thể σ2
- Dạng 2: Kiểm định 2 Trung bình tổng thể μ (chỉ rơi vào trường hợp khi chưa biết 2 phương sai σ2)
- Dạng 3: Kiểm định 1 Tham số P (Khi kích thước mẫu n > = 100)
- Dạng 4: Kiểm định 2 Tham số P (2 mẫu đề cho đều là mẫu lớn)
- Dạng 5: Kiểm định 1 Phương sai tổng thể σ2 (Đề thi chỉ ra khi chưa biết trung bình tổng thể μ)
- Dạng 6: Kiểm định giả thiết 2 Phương sai tổng thể σ2
Xem hình:
- 5 BẪY KHI ĐI THI MÔN XÁC SUẤT
Toàn bộ tất cả các bẫy của môn xác suất của tất cả các trường từ Đại học cho đến Cao học đều được tổng kết ở đây:
- BẪY 1: Đề ra suy diễn tần suất mẫu f
f = X/n
. X --> min thì --> f min
. X --> max thì --> f max
- BẪY 2: Đề ra ước lượng tham số P
P = X/N
. N --> max thì P --> min
. N --> min thì P --> max
Chú ý: Đây là những bài toán rất khó của học phần thống kê, các bạn phải được rèn luyện vài bài thì mới nắm chắc được dạng bẫy 2.
- BẪY 3: Đề kiểm tra ý nghĩa của Phương sai tổng thể σ2
Đây là bẫy rất ưa thích ra của môn Toán kinh tế cao học Học viện ngân hàng vì có những năm đề thi đã ra cả 2 đợt thi và cũng thường xuyên thi.
Sau đây Thầy Mạnh sẽ hướng dẫn các bạn vượt qua bẫy số 3 bằng các kiến thức xác suất chuyên sâu:
Đầu tiên bạn phải hiểu ý nghĩa của Phương sai
-
Ý nghĩa: Phương sai phản ánh Độ phân tán, Độ mất ổn định, Độ mất chính xác, Độ biến động giữa giá trị của biến ngẫu nhiên so với giá trị trung bình. Do đó, có thể hiểu phương sai mà càng lớn thì càng không tốt.
Từ Ý nghĩa mà thầy đã viết rất dễ hiểu ở trên thì ta có:
ĐÁP ÁN thi như sau:
-
Độ đồng đều giảm sút -- > Tức là Độ phân tán tăng lên
-
Độ ổn định giảm sút -- > Tức là Độ mất ổn định tăng lên
-
Độ chính xác giảm sút -- > Tức là Độ mất chính xác tăng lên
-
Độ an toàn giảm sút -- > Tức là Độ rủi ro tăng lên
Mặc dù, các bạn được cung cấp hết đáp án của các năm như ở trên, tuy nhiên cần phải hiểu các ý nghĩa, khái niệm để đề thi ra kiểu gì, xoay kiểu gì ta vẫn làm được.
- BẪY 4: Đề thi sẽ làm khó ở cặp giả thuyết
Phần Kiểm định có thể coi là dễ nhất của môn Xác suất thống kê, vì các bạn chỉ cần chép lại công thức và thay số, sau đó ấn máy tính.
Tuy nhiên, nếu ngay từ đầu mà chúng ta xác định cặp giả thuyết sai thì miền bác bỏ w anpha sai, thay số vào sai nên rất nguy hiểm. Do đó các bạn cần đọc kỹ đề và có thao tác kiểm tra cặp giả thiết: Ho, H1 xem chúng có đối nhau không.
- BẪY 5: Kiểm định P = M/N là Không thi nhé các bạn.
Để có thể Ôn thi tốt môn Toán kinh tế Cao học Học viện ngân hàng T4.2018 các bạn tham khảo:
Video: HƯỚNG DẪN GIẢI ĐỀ THI TOÁN KINH TẾ CAO HỌC HVNH T8.2013
5. Đáp án thi học phần Quy hoạch tuyến tính
Trung tâm đã có những biết viết chuyên sâu về Đáp án thi học phần Quy hoạch tuyến tính. Các bạn xem chi tiết tại đây:
Làm thế nào đạt Điểm 10 môn Quy hoạch Tuyến tính?
Câu 1 (2 điểm): Giải bài toán bằng phương pháp đơn hình (3 Dạng)
- Dạng 1: Bài toán ở dạng chuẩn (rất ít thi)
- Dạng 2: Bài toán không ở dạng chuẩn và đề bài cho 1 PACB Xo (ít ra)
- Dạng 3: Bài toán không ở dạng chuẩn và đề bài không cho 1 PACB Xo (HAY THI). Khi đó các bạn phải lập bài toán phụ: P(x, xg) --> min.
- 5 khái niệm của môn Quy hoạch tuyến tính các bạn xem như hình:

- Cách trình bày một bài thi Quy hoạch tuyến tính max điểm các bạn xem như hình dưới:

Câu 2 (2 điểm): Bài toán đối ngẫu.
- Dạng 1: Đề bài cho bài toán xuất phát từ f(x) --> Tìm f~(y).
- Dạng 2: Bài toán ngược từ f~(y) --> Tìm f(x) .
Xem chi tiết Bài toán đối ngẫu:

Xem đáp án và cách trình bày 1 bài mẫu ở đây:
Đáp án thi cao học Toán kinh tế HVNH BA T8.2013
Hi vọng với những chia sẻ đầy tâm huyết của Thầy Mạnh sẽ giúp các bạn có những kiến thức tốt nhất để trang bị trước kỳ thi.
Chúc các bạn đạt thành tích cực cao học kỳ thi Cao học Học viện Ngân hàng T4.2018.
Trân trọng !
Bình luận (4):
Khuê
Em tốt nghiệp hvnh cũng khá lâu rồi ạ. Mà muốn thi cao học không biết cần ôn luyện lâu không ạ. Thầy gửi tài liệu giúp em địa chỉ mail Dudaikhue@gmail.com Em cảm ơn thầy
ĐÀO ĐỨC ANH
Thầy ơi, bài viết rất cụ thể và chi tiết và em cám ơn thầy Mạnh vì các kiến thức thầy dạy và chia sẻ với em. + Email của em là anhdd.bsc@gmail.com
Nguyễn Thế Mạnh
Hoàng Thảo: Em sẽ có những đáp án môn Kinh tế học chất lượng cho kỳ thi cao học DDHKT-ĐHQG HN T4.2018. Thầy sẽ gửi cho e trong ít phút
Hoàng Thảo
Thầy Mạnh là một giáo viên tâm huyết, có kiến thức và kỹ năng sư phạm cực tốt. Mỗi buổi học tuy kiến thức khá nhiều nhưng chưa bao giờ nhàm chán mà ngược lại rất vui vẻ, dễ chịu. Tuy thời gian học thầy chưa được nhiều nhưng nhờ nắm được bí kíp và chiến thuật làm bài thầy hướng dẫn nên em cảm thấy tự tin trước kỳ thi sắp tới. Email của em là: nguyenhoangthaohp93@gmail.com. Em cám ơn thầy nhiều ạ!
